Archive
Python: Digit fifth Powers
Python: Digit Fifth Powers
Projecteuler Problem No.30
This was an easy task and I solve it on my mobile during a brain resting session 😜. I will just copy the problem statement as it is in ProjectEuler ..
Surprisingly there are only three numbers that can be written as the sum of fourth powers of their digits:1634 = 14 + 64 + 34 + 44
8208 = 84 + 24 + 04 + 84
9474 = 94 + 44 + 74 + 44As 1 = 14 is not a sum it is not included.
The sum of these numbers is 1634 + 8208 + 9474 = 19316.Find the sum of all the numbers that can be written as the sum of fifth powers of their digits.
Read it on Projecteuler
My Problem When I start solving the task i was wondering how far i should check the numbers? We can’t just go for ever, we must stop in some range. I search the web for such cases an i fond a post that clearing this with a formula. I will explain this in my way.
Finding the Upper Limits:
1. We are talking about Power (P=5)
2. We are using the (Base ten) numbers, so the highest digit is 9. Then:
3. 9 power 5 (9p5 = 59049)
4. The digits in (59049) are D=5.
5. Finally, The Formula is (D * 9p5), 5 * 59049 = 295245
6. So, The Upper Limits = 295245

|
According to the “Finding the Upper Limits” section, if we want to use the power (4) then the upper limit will be:
9p4 = 6561
6561 is a 4 digits
upper limit = 4 * 6561 = 26244
The Code: [The code is for power 4]
# Digit Fifth Powers
# Projecteuler Problem 30
num = 2
pdig = []
wefound = []
thesum = 0
while num < 26244 :
for each in str(num):
pdig.append(int(each) ** 4)
for x in pdig:
thesum = thesum + int(x)
if thesum == num:
wefound.append(num)
print(‘\n Number =’, num)
print(‘ Digits Power 4 =’, pdig)
print(‘ The Sum ‘, thesum)
num = num + 1
pdig = []
thesum = 0
thesum = 0
for x in wefound:
thesum = thesum + x
print(“\n The Numbers that the 4th power of its each digit = itself are: “,wefound)
print(” The Sum of the numbers is: “,thesum)

|
 Follow me on Twitter.. Follow me on Twitter.. |
Python: Self Power
Python: Self Powers
Problem No.48 on ProjectEuler
Another easy task in Problem No.48. We have to find the power of each number to itsefl in the range of 1 to 1000 and get the sum of all numbers, then to find the last ten digits of the series.
In this Task we will save the powers in a set name powers then we run a for loop
to get the sum of all elements in the lest, later will reade the last ten digits.
Enhancment In this problem I will not do any more than solving the problem, but if we want to enhance the project, we can ask the user to enter a range and we perform the function on that range of numbers.

|

|
The Code:
powers=[]
def get_power(num):
powers.append(num**num)
for x in range(1,1001):
get_power(x)
sum=0
for each in powers:
sum=sum+each
print(powers)
print (‘the sum is ‘,sum)
Python : Curious Number
Python: Curious Number
Problem No.34 in ProjectEuler
Definition: A number is Curious Number if the factorial of their digits equal to the number itself.
Example: 145 is a curious number, as 1! + 4! + 5! = 1 + 24 + 120 = 145.
Our Task: We will write two functions, first one will get (return) all digits in the number, then another function to get the factorial of each digits in that number then with If statement we will examine the result.Enhancement: We will ask the user to enter a number and we will check if it is a Curious Number.
We will reuse some of our functions that we wrote in previous posts.
The Code:
digs=[]
print(‘\nEnter a number to see if it is a Curious Number or not.’)
num=input (‘\nEnter a number: ‘)
num=input (‘Enter a number: ‘)
tot=0
# To get the digits In a number
def digits_in_num (num):
for each in str(num):
digs.append(each)
# To get the Factorial of a number
def Factorial_digit_sum(num):
if (num == 0) :
return 1
else:
return num * Factorial_digit_sum(num-1)
for each in digs:
print(‘factorial :’,each,’ is ‘,Factorial_digit_sum(int(each)))
tot = tot + Factorial_digit_sum(int(each))
print(‘\nTotal sum of the Factorial of each digits is: ‘,tot)
if int(num) == tot:
print(num ,’Is a Curious Number.’)
else:
print(num ,’Is NOT Curious Number.’)
Python: Multiples of Numbers
Python: Multiples of 3 and 5
Problem No.1 in ProjectEuler
This is very easy, very short task to work on, the task as is in ProjectEuler like this “Find the sum of all the multiples of 3 or 5 below 1000.”
My way, as i like to do open code works for any numbers, we will ask the user to enter three numbers, num1 and num2 will be as (3 and 5) in the task, my_range will be as the 1000. So the code can get the sum Multiples of any two numbers in a ranges from 1 to my_range.
The Code:
# Multiples of 3 and 5
# ProjectEuler: Problem 1
def Multiples_of_N (num1,num2,my_range):
tot=0
for t in range (1,my_range):
if t %num1==0 or t%num2 ==0 :
tot = tot + t
return tot
print ‘\nDescription: This function will take three variables, two numbers represint the what we want to get there Multiples, then we ask for a range so we will start from 1 to your range.\n’
num1=int(input(‘Enter the first number:’))
num2=int(input(‘Enter the second number:’))
my_range =int(input(‘Enter the range (1, ??):’))
total=Multiples_of_N (num1,num2,my_range)
print ‘\nYou entered ‘,num1,’,’, num2,’ So the sum of all multiples of those number in range (1-‘,my_range,’) = ‘,total
Python: Largest product in series
Python: Largest product in a series
Problem 8 @ projectEuler
In Problem 8, ProjectEuler wants to find the thirteen adjacent digits in the 1000-digit number that have the greatest product.
In this task i use a for loop to check each 13-dig set, each time creating a set of 13 digits starting from (0,13) then (1,14)..(2,15)….. and so-on. for each set i get the product of its digits and store it in an a array of [set,total] each time if total of the new set is larger than what we have in the array[total] then we write the new values to the array, we call the array largest.
The Code:
# Largest product in a series
# ProjectEuler: Problem 8
num=’7316717653133062491922511967442657474235534919493496983520312774506326239578318016984801869478851843858615607891129494954595017379583319528532088055111254069874715852386305071569329096329522744304355766896648950445244523161731856403098711121722383113622298934233803081353362766142828064444866452387493035890729629049156044077239071381051585930796086670172427121883998797908792274921901699720888093776657273330010533678812202354218097512545405947522435258490771167055601360483958644670632441572215539753697817977846174064955149290862569321978468622482839722413756570560574902614079729686524145351004748216637048440319989000889524345065854122758866688116427171479924442928230863465674813919123162824586178664583591245665294765456828489128831426076900422421902267105562632111110937054421750694165896040807198403850962455444362981230987879927244284909188845801561660979191338754992005240636899125607176060588611646710940507754100225698315520005593572972571636269561882670428252483600823257530420752963450
‘
v1=0
v2=13
set1=num[v1:v2]
largest =[0,0]
tot=1
for x in range((1000)):
set1=num[v1:v2]
for each in set1:
tot=tot * int(each)
if tot > largest [1]:
largest[0] = set1
largest[1] = tot
tot=1
tot =1
v1=v1+1
v2=v2+1
print’The thirteen adjacent digits are’,largest[1],’there product is ‘,largest[0]
Python: Factorial Digit Sum
Python: Factorial Digit Sum
Problem 20 @ projectEuler
The Task: The task in projectEuler P20 is to get the sum of the digits in the number Factorial of 100!
Factorial NdefinitionThe factorial of a positive integer n, denoted by n!, is the product of all positive integers less than or equal to n. For example, 10! = 10 × 9 × … × 3 × 2 × 1 = 3628800.
Problem 20 is another easy problem in projectEuler, and we will write two functions to solve it. First one is a Factorial_digit_sum this one will return the factorial of a number. The second function will calculate the sum of all digits in a number N and we will call it sum_of_digits.
Clarification As long as i just start solving or posting my answers to projectEuler portal, i am selecting problems and not going through them in sequence, that’s way my posts are jumps between problems, so if i am posting the code to solve problem 144 (for example) that does’t meaning that i solve all problems before it.
print of solved screen:

The Code:
#Python: Factorial Digit Sum
#Problem No.20 on projectEuler
def Factorial_digit_sum(num):
if (num == 0) :
return 1
else:
return num * Factorial_digit_sum(num-1)
num=100
fact =Factorial_digit_sum(100)
print fact,’is the Factorial of {}.’.format(num)
def sum_of_digits(dig):
t = 0
for each in dig:
t = t + int(each)
print ‘\nThe sum of your number is’,t
sum_of_digits(str(tot1))
Python: Collatz Sequence
Python: Longest Collatz Sequence
Problem No.14 in ProjectEuler
Definition Wikipedia: Start with any positive integer n. Then each term is obtained from the previous term as follows: if the previous term is even, the next term is one half the previous term. If the previous term is odd, the next term is 3 times the previous term plus 1. The conjecture is that no matter what value of n, the sequence will always reach 1.
So the formula is: Starting with n, the next n will be:
n/2 (if n is even)
3n + 1 (if n is odd)
If we start with 13, we generate the following sequence:
13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1.
A walk through:
n=13, 13 is odd, then n = 13 * 3 + 1 , n= 40
n=40, 40 is even, then n= 40/2, n=20
n=20, 20 is even, then n=20/2, n=10
n=10, 10 is even, then n=10/2, n=5
n=5, 5 is odd, then n=5*3+1 , n=16
n=16, 16 is even, then n=16/2, n=8
n=8, 8 is even, then n=8/2, n=4
n=4, 4 is even, then n=4/2, n=2
n=2, 2 is even, then n=2/2, n=1
n=1 then end of sequence
The Task: The task in ProjectEuler is to searching for a the Number N, under one million, that produces the longest chain.
Overview to my python cases: In my company, we are not allowed to download any software, so i don’t have any Python platform. To solve this i am using an online python interpreter, some time it’s become slow. So in this code (and others) i am spiting the range in 10 each with 100,000 then running the code to get the longest chain in each range. So the Number N, under one million, that produces the longest chain is:
The Answer: In my previous codes or math solving challenges in pybites or ProjectEuler I am solving the problems, writing the code, but not posting my answer to ProjectEuler platform. Today, and with Problem No.14 i decide to post the answer in the ProjectEuler platform for the first time just to see what will happen. The answer was 837799, and I get this page.
In the code bellow, i set the range from 1 to 50000.
The Code:
chain2=[]
longest=[0,0]
def collatz_Seq(num):
t= num
chain=[num]
while t !=1 :
if t%2==0:
t=t/2
chain.append(int(t))
else:
t=3*t+1
chain.append(int(t))
return chain
for num in range (1,50000):
chain2 = collatz_Seq(num)
if len(chain2) > longest[0]:
longest[0] = len(chain2)
longest[1] = num
chain2=[]
print(‘num:’,longest[1],’ has a longest chain: ‘,longest[0])
Python: The Factors
Python: Factors of the Number N
This is a short task to get the factors of a given number. The Definition of Factors of N is: The pairs of numbers you multiply to get the N number.
For instance, factors of 15 are 3 and 5, because 3×5 = 15. Some numbers have more than one factorization (more than one way of being factored). For instance, 12 can be factored as 1×12, 2×6, or 3×4
In this task we will write a Python code to ask the user for a number N then will get all the pairs number that if we multiply them will get that N number, we will store the pairs in a array ‘factors’.
The Code:
def factors_of_n(num):
a=1
factors=[]
while a <= num:
if num%a==0:
if (num/a,a) not in factors:
factors.append((a,int(num/a)))
a = a + 1
return factors
#Ask the user for a number
num=int(input(“Enter a number: “))
print(factors_of_n(num))
Python: Amicable Numbers
Python: Amicable Numbers
Problem No.21 on projectEuler
In this task we need to calculate the SUM of all divisors of N, from 1 to N.
Then we calculate the Sum of (sum of N divisors ) let’s say M .
Now if
For example, the proper divisors of A=220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110; therefore F(220) = 284. And the proper divisors of B=284 are 1, 2, 4, 71 and 142; so F(284) = 220. So F(A) =B and F(B)=A then A and B are amicable.
Definition:
If f(a) = b and f(b) = a, where a ≠ b, then a and b are an amicable pair and each of a and b are called amicable numbers.
In this task we will ask the user to enter a Range of numbers and we will search for all Amicable Numbers pairs in that range(from – to) if we fond one we will print out the number and the divisors list. The main function here is the one that get the sum of divisors, we will call it get_divisors_sum and we will examine Amicable with If statement.
Hint ..
To check if the sum of divisors from both said are equal we use (t2==x )
AND that this sum are not same we use (t1!=t2)
AND that we did not print the pair before we use: (t2 not in ami_pair)
The Code:
#Python: Amicable Numbers
#Problem No.21 on projectEuler
num1=int(input(‘The range Start from:’))
num2=int(input(‘The range Ends at:’))
t1=0
t2=0
l=[]
l1=[]
l2=[]
ami_pair=[]
def get_divisors_sum (num):
t=0
l=[]
for a in range (1,num):
if num%a==0 :
l.append(a)
t=t+a
return t,l
for x in range(num1,num2):
l1=[]
t1,l1=get_divisors_sum(x)
l2=[]
t2,l2=get_divisors_sum(t1)
if (t2==x) and (t1!=t2) and (t2 not in ami_pair):
print(‘\nget_divisors_sum({}) is {} divisors={}’.format(x,t1,l1))
print(‘\nget_divisors_sum({}) is {} divisors={}’.format(t1,t2,l2))
print(‘\nSo {} and {} are Amicable Numbers .’.format(t1,t2))
ami_pair.extend((t1,t2))
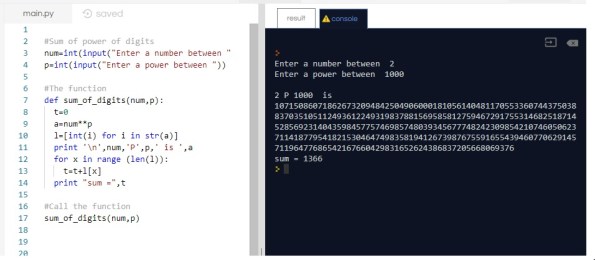
Python Project: Sum of power of digits
Python: Sum of power of digits
Problem No.16
In Problem No.16, projectEuler ask to find the Sum of power of digits in the number, for example if we have 2^15 (2 to power of 15) the answer is 23768 then we need to calculate the sum of this number (2+3+7+6+8 ) that’s equal to 26.
The Task: So our task in this project is to find the sum of the digits of (2^1000). To write this as a program and to make it more general we will ask the user to input the number and the power he want, then I start thinking to restrict user from input large numbers that could cause CPU problems, but then i decide to keep it open as is.
The Code:
num=2
p=15
num=int(input(“Enter a number “))
p=int(input(“Enter a power “))
a=num**p
def sum_of_digits(num,p):
a=num**p
l=[int(i) for i in str(a)]
print(l)
for x in range (len(l)):
t=t+l[x]
print (“sum =”,t)