Archive
Python: Permuted Multiples
Python: Permuted Multiples
Problem No.52 @ Projecteuler
This task Completed on Mon, 1 Jul 2019, 06:08, the goal is to find a number X that if we get the X, X*2, X*3, X*4, X*5, X*6 all the numbers are same digits but in a different order.
I use a function called if_x_in_y (n1,n2) will return True if the two numbers has same digits, False if not. Then a while found_one is not True a loop will examine all numbers starting from 2 until we found_one.

|
The Code:
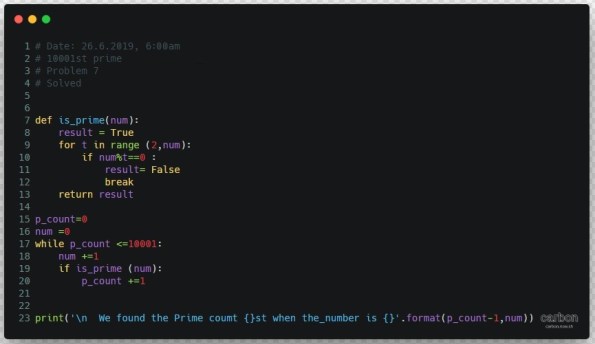
# Projecteuler.net
# Permuted multiples
# Problem No.52
# Completed on Mon, 1 Jul 2019, 06:08am (GMT+3)
# if x, x*2, x*3, x*4, x*5, x*6 has the same digits.
def if_x_in_y (n1,n2) :
for x in str(n1) :
if x not in str(n2) :
return False
for x in str(n2):
if x not in str(n1):
return False
return True
x_num = 2
found_one= False
while not found_one:
if if_x_in_y(x_num,x_num*2):
if if_x_in_y(x_num,x_num*3):
if if_x_in_y(x_num,x_num*4):
if if_x_in_y(x_num,x_num*5):
if if_x_in_y(x_num,x_num*6):
print(‘\n Yes, we found one ..’)
found_one = True
print(‘ The Number is ‘,x_num)
x_num += 1
print(x_num,x_num*2,x_num*3,x_num*4,x_num*5,x_num*6)
|
Python: Number Letter Counts
Python: Number Letter Counts
Problem 17, Projecteuler
For problem 17, projectEuler ask for the total numbers of alphabetics in all words of numbers from 1 to 1000.
Here I am coping from there page.
Once I read the task, I decide to create my own version of the requirement. I start to assume that I may have a dictionary with some numbers and words, then base on what ever the user will input (number between 1 and 999) then I shall convert it to words.
Example:
1 –> one
8 –> eight
234 –> tow hundred thirty-four .. and so on.
I start searching the net to get the words I need, and store them in 3 dictionaries.
num_1_9 = {“1″:”one”,”2″:”two” .. ext.
num_10s = {“10″:”ten”,”20″:”twenty” .. ext.
num_11s = {“11″:”eleven”,”12″:”twelve”.. ext
Then, I start writing the functions for each group of numbers/dictionaries, so if the user enter a number we will read number of digits if it is 1 then we call def num_1_d(), if it is 2 digits we call def num_2_ds() and if it is 3 digits we call num_3_ds(). At the end, we got the right answer for Projecteuler, and here is the code in my way, I am asking the user to enter a number then i convert it to a corresponding words.

|
The Code:
# Date:27/6/2019
# ProjectEuler
# Problem No.17
# Completed on Sun, 30 Jun 2019, 10:30
num_1_9 = {“1″:”one”,”2″:”two”,”3″:”three”,”4″:”four”,”5″:”five”,”6″:”six”,”7″:”seven”,”8″:”eight”,”9″:”nine”}
num_11s={“11″:”eleven”,”12″:”twelve”,”13″:”thirteen”,”14″:”fourteen”,”15″:”fifteen”,”16″:”sixteen”,”17″:”seventeen”,”18″:”eighteen”,”19″:”nineteen”}
num_10s ={“10″:”ten”,”20″:”twenty”,”30″:”thirty”,”40″:”forty”,”50″:”fifty”,”60″:”sixty”,”70″:”seventy”,”80″:”eighty”,”90″:”ninety”}
num_100=’hundred’
def num_1_d(num):
if len(str(num)) == 1:
return num_1_9[str(num)]
def num_2_ds(num):
d0,d1 = num[0], num[1]
if int(num[1])== 0 :
return num_10s[str(num)]
elif int(num[0]) == 1 :
return num_11s[str(num)]
elif (int(num[0])) >1 :
d0=str(d0)+str(0)
return ‘{}-{}’.format(num_10s[str(d0)],num_1_9[str(d1)])
def num_3_ds (num):
d0,d1,d2=num[0],num[1],num[2]
if (int(num[1])==0) and (int(num[2])==0) :
return ‘{} {}’.format(num_1_9[str(d0)],num_100)
elif (int(num[1])>0):
d1 = str(d1)+str(d2)
return ‘{} {} and {}’.format(num_1_9[str(d0)],num_100,num_2_ds(d1))
elif (int(num[1])==0) and (int(num[2])>0):
d1 = str(d1)+str(d2)
return ‘{} {} and {}’.format(num_1_9[str(d0)],num_100,num_1_9[str(d2)])
num =0
while num !=’f’ :
num =input(‘\nEnter a number: (1-999)’)
if len(str(num)) == 1:
print(num ,’ is ‘,(num_1_d(num)))
elif len(str(num)) == 2:
print (num ,’ is ‘,(num_2_ds(num)))
elif len(str(num)) == 3:
print (num ,’ is ‘,(num_3_ds(num)))
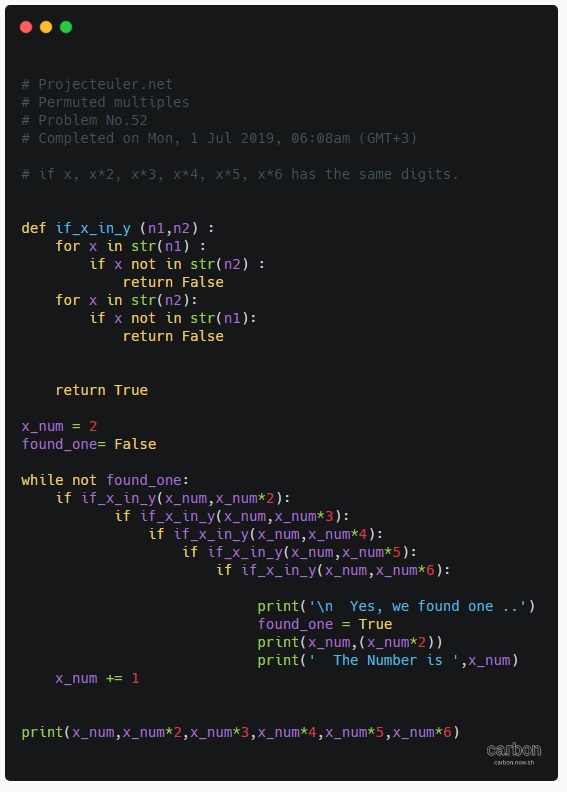
This is Output screen for my-way version
|
Python: 10001st Prime
Python: 10001st Prime
Problem No.7 @ ProjectEuler
This is one of shot projects you may find on ProjectEuler, the task is find the prime No 10001, I just run my is_prime function, if the number is prime will add 1 to the counter, until we reach 10001, that will be the answer.

|
The Code:
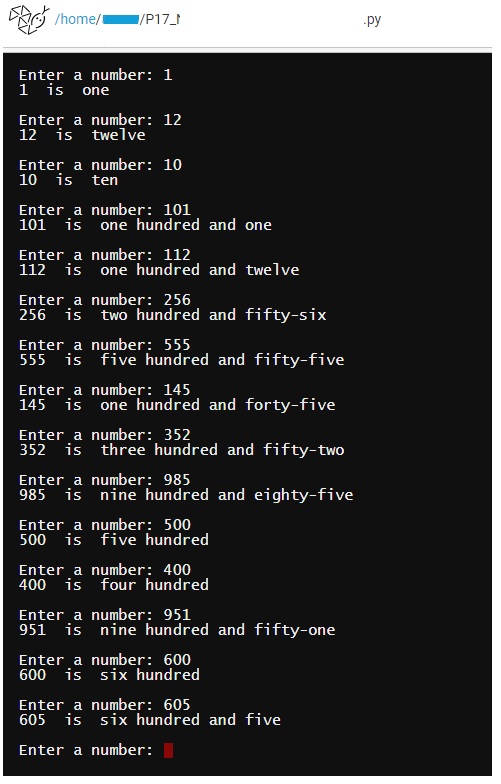
# 10001st prime
# Problem 7
# Solved: Wed, 26 Jun 2019, 05:57am (GMT+3)
def is_prime(num):
result = True
for t in range (2,num):
if num%t==0 :
result= False
break
return result
p_count=0
num =0
while p_count <=10001:
num +=1
if is_prime (num):
p_count +=1
print(p_count,num)
print(num,p_count-1)
Python: Largest Prime Factor
Python: Largest Prime Factor
Problem No.3 on ProjectEuler
Quite easy one to solve, in this task we need to get all the factors of a given number, then to print out the largest prime one.

|
To solve this with a Large Number I search the net and i fond an article explain it. So here i am putting it in points.
Factors of Large Numbers:
1. First ask if the number N is (Even or Odd)?
2. If the number N is Even, then factors=(2) then, the new N = N Divide by 2.
3. If the number N is Ood, then start form 3 and get/find smallest prime factors (SPF) of it.
4. Add the smallest prime factors to factors list.
5. Then, the new N = N Divide by smallest prime factors (SPF).
6. If the new N is Even goto line 2, If the new N is Odd goto line 3.
The Code:
# Largest prime factor
# Problem No.3
# Solved
def factors_of_n(num):
a=3
while a <= num:
if num%a==0:
return int(a)
break
a = a + 1
# This is the number from ProjectEuler
num = 600851475143
temp_num = num
facto_back =0
p_factors =[]
the_num=1
while temp_num > 1 :
if temp_num%2==0 :
p_factors.append(2)
temp_num = temp_num / 2
else:
facto_back =factors_of_n(temp_num)
p_factors.append(facto_back)
temp_num = temp_num / facto_back
print(p_factors)
print(‘\n Largest Prime Factor of {} is {}’.format(num,max(p_factors)))

|
Python Project: Split and join
Python: Split and join
Split up the message on newline
The target of this task is to Split a given text message on the newline (\n) then use the join builtin to stitch it together using a ‘|’ (pipe).
I fond this on the pybites web-site as a code-challenges bites #104. In our case we will print the new Message within the function but we can return it back as a variable for more usage in our code..
Enhancements: If we want to do some enhancements to this code:
1. We can read the message from a file.
2. Letting the user to select the joining character.
3. Also we may export the final message to another txt file.
We assume our message is “Hello world!\nWe hope that you are learning a lot of Python.\nHave fun with our Bites of Py.\nKeep calm and code in Python!\nBecome a PyBites ninja!”
The Code:
def split_in_columns(message=message):
sp_message = message.split(“\n”)
message=”|”.join(sp_message)
print(message)
split_in_columns(message=message)
Python: Digit Factorial Chains
Python: Digit factorial Chains
Problem No.74 @ ProjectEuler
In this task, we need to produce a chain of the summation of a factorial number and keep chasing each number in the chain until it starts repeat, we stop there and count the length of the chain, if its 60 then we increase a counter. ProjectEuler task 74 ask to do this and get all the numbers (How many are they?) below one Million (1000000) that has 60 numbers in it’s chain.
So we start to write two functions, one to get the factorial of a number, and the other to get the summation of the numbers in a list. Then with two (while) loop, an outer one to count the 60’s chain numbers, and an inner one to produce the chains.
At the end we manage to solve the problem 74 using Pythonanywhere.

|
The Code:
#Digit factorial chains
#Problem 74
numbers=[]
# Function to get the Factorials of a number.
def get_factorial(num):
if (num == 0) :
return 1
else:
return num * get_factorial(num-1)
def get_summation(the_list):
tot=0
for each in the_list:
tot +=each
return tot
start_num = 2
the_num = start_num
keep_chain=[start_num]
chain_count = 0
print(‘We start with number ‘,start_num)
the_facto_d_sum = 0
while start_num < 1000000 :
the_num = start_num
keep_chain=[start_num]
while the_facto_d_sum != start_num:
for each in str(the_num):
numbers.append(get_factorial(int(each)))
the_facto_d_sum = get_summation(numbers)
the_num = the_facto_d_sum
if the_num in keep_chain :
the_facto_d_sum = start_num
else:
keep_chain.append(the_num)
numbers=[]
if len(keep_chain) == 60:
chain_count +=1
keep_chain =[]
start_num +=1
print(‘we have {} numbers with 60 ‘.format(chain_count))
Python: Multiples of Numbers
Python: Multiples of 3 and 5
Problem No.1 in ProjectEuler
This is very easy, very short task to work on, the task as is in ProjectEuler like this “Find the sum of all the multiples of 3 or 5 below 1000.”
My way, as i like to do open code works for any numbers, we will ask the user to enter three numbers, num1 and num2 will be as (3 and 5) in the task, my_range will be as the 1000. So the code can get the sum Multiples of any two numbers in a ranges from 1 to my_range.
The Code:
# Multiples of 3 and 5
# ProjectEuler: Problem 1
def Multiples_of_N (num1,num2,my_range):
tot=0
for t in range (1,my_range):
if t %num1==0 or t%num2 ==0 :
tot = tot + t
return tot
print ‘\nDescription: This function will take three variables, two numbers represint the what we want to get there Multiples, then we ask for a range so we will start from 1 to your range.\n’
num1=int(input(‘Enter the first number:’))
num2=int(input(‘Enter the second number:’))
my_range =int(input(‘Enter the range (1, ??):’))
total=Multiples_of_N (num1,num2,my_range)
print ‘\nYou entered ‘,num1,’,’, num2,’ So the sum of all multiples of those number in range (1-‘,my_range,’) = ‘,total
Python: Factorial Digit Sum
Python: Factorial Digit Sum
Problem 20 @ projectEuler
The Task: The task in projectEuler P20 is to get the sum of the digits in the number Factorial of 100!
Factorial NdefinitionThe factorial of a positive integer n, denoted by n!, is the product of all positive integers less than or equal to n. For example, 10! = 10 × 9 × … × 3 × 2 × 1 = 3628800.
Problem 20 is another easy problem in projectEuler, and we will write two functions to solve it. First one is a Factorial_digit_sum this one will return the factorial of a number. The second function will calculate the sum of all digits in a number N and we will call it sum_of_digits.
Clarification As long as i just start solving or posting my answers to projectEuler portal, i am selecting problems and not going through them in sequence, that’s way my posts are jumps between problems, so if i am posting the code to solve problem 144 (for example) that does’t meaning that i solve all problems before it.
print of solved screen:

The Code:
#Python: Factorial Digit Sum
#Problem No.20 on projectEuler
def Factorial_digit_sum(num):
if (num == 0) :
return 1
else:
return num * Factorial_digit_sum(num-1)
num=100
fact =Factorial_digit_sum(100)
print fact,’is the Factorial of {}.’.format(num)
def sum_of_digits(dig):
t = 0
for each in dig:
t = t + int(each)
print ‘\nThe sum of your number is’,t
sum_of_digits(str(tot1))
Python Project: Armstrong Numbers
Python: Armstrong Numbers
Check for Armstrong number in a range
In our last post (‘Check if a Number is Armstrong‘) we wrote a codes to check a given number and see whether it is an Armstrong or Not.
Today, we want to go through a set of numbers and see how many Armstrong numbers are there.
Before calling the ‘armstrong_in_range()’ and just to keep the code as less as we can, I assume the two numbers has the same number of digits, also I am getting the power (p) and the range numbers (n1, n2) out-side of this function and passing all as variables.
def armstrong_in_range(p,n1,n2):
my_sum = 0
count = 0
for num in range (n1,n2):
tot=num
for arm in range(p):
my_sum = my_sum + ((num % 10)**p)
num = num // 10
if my_sum == tot:
print(‘\nThe number {} is Armstrong.’.format(tot))
my_sum=0
count = count +1
else:
my_sum=0
print(‘\nWe have {} armstrong number(s)’.format(count))
Python Project: IF N an Armstrong
Python: Armstrong Numbers
Check if a Number is Armstrong
In late nineties, I was programming using Pascal Language and I was very passionate to convert some mathematical syntax into codes to fine the result, although some of them were very easy; but the goal was to write the codes.
Today, we are attempted to write a code in Python to check whether a number is an Armstrong or Not. First let’s ask:what is Armstrong number?Answer: If we assume we have a number (num = 371), 371 is an Armstrong because the sum of each digits to the power of (number of the digits) will be the same. That’s mean 371 is a three digits so the power (p=3) so:
3**3 = 27
7**3 = 343
1**3 = 1
then (27+343+1) = 371. … So 371 is an Armstrong Number.
In wikipedia:
Armstrong also known as a pluperfect digital invariant (PPDI) or the Narcissistic number is a number that: the sum of its own digits each raised to the power of the number of digits equal to the number its self.
# Function to check whether a number is Armstrong or Not.
def is_it_armstrong(num):
p= len(str(num)) # First: we get the power of the number
my_sum=0
tot=num
for x in range (p) :
my_sum=my_sum+((num%10)**p)
num=num//10
if my_sum == tot:
print(‘\nThe number {} is Armstrong.’.format(tot))
else :
print(‘\nThe number {} is NOT Armstrong.’.format(tot))
 Follow me on Twitter..
Follow me on Twitter..