Archive
Python: Largest Palindrome Product
Python: Largest Palindrome Product
Problem No.4 @ Projecteuler
Complete on: on Fri, 5 Jul 2019, 08:53
The task was to find the largest palindromic number that been generated from multiplying two of 3 digits number.
Definition: Palindromic numbers are numbers that remains the same when its digits are reversed. Like 16461, we may say they are “symmetrical”.wikipedia.org
To solve this I first wrote a function to check if we can read a number from both side or not, Then using while and for loop through numbers 100 to 999, and store largest palindromic, we select the range (100,999) because the task is about tow number each with 3 digits.

|
The Code:
# Problem 4
# Largest palindrome product
# SOLVED
# Completed on Fri, 5 Jul 2019, 08:53
palin =0
def palindromic(n) :
n_list=[]
for each in str(n) :
n_list.append(each)
n_last = len(n_list)-1
n_first =0
x=0
while (n_first+x != n_last-x) :
if n_list[n_first+x] != n_list[n_last-x] :
return False
else :
x +=1
if (n_first +x > n_last -x):
return True
return True
for set1 in range (1,999):
for set2 in range (set1,999):
if palindromic(set1 * set2) :
if (set1 * set2) > palin :
palin =(set1*set2)
print(‘\n We found it:’,palin, ‘coming from {} * {}’.format(set1,set2))

|
Python: Champernowne’s constant
Python: Champernowne’s constant
Problem No.40 @ ProjectEuler
Completed on: Mon, 1 Jul 2019, 18:01
In This task No.40, basically we need to get some digits from a large decimal fraction, then finding the multiplication of those digits.
ProjectEuler assume that the fraction is: 0.123456789101112131415161718192021222324 …. until 1000000, then we should fined the digits in positions 1, and 10, 100, 1000, 10000, 100000 and 1000000. Here is a copy of the problem screen

|
So to solve this I create a string variable n_list then using for loop i store the numbers from 1 to 1000000 in it as [12345678910111213141516 … 1000000], and simply get the digits I want using the list index, and Finally I calculate the needed multiplication as required. .. And we solve it. ..

|
Python: Combinatoric Selections
Python: Combinatoric Selections
Problem 53 @ projecteuler
Completed on: Mon, 1 Jul 2019, 11:32
This is one of the tasks that based on equations. To solve this, first let me Simplify it.
Simplifying the task:
if 1<= n <= 100 , and r <= n
using the equation of C(n,r) is
c(n,r) = n! / (r! *(n-r)!
How many values of c(n,r) greater than one-million
Since we need the factorial of n (n!) and (r!) then I will re-use our function get_factorial(num), and I will write another function to calculate the C(n,r) as in the equation above, I will call it combi(n,r), also I will use a while loop, and we need to set some variables to help us in the execution. In this part, I will use a list called values_over_1m to store all the values in it, although this is Not required in the Problem 53, but i will keep it so later we can print them all to the screen or just get the total values of it. And so we did .. and we get the right answer.
|
The Code:
# Combinatoric selections
# Problem 53 @ projecteuler
# Completed on Mon, 1 Jul 2019, 11:32
”’
if 1<= n <= 100 , and r <= n
using the equation of C(n,r) is
c(n,r) = n! / (r! *(n-r)!
How many values of c(n,r) greater than one-million
'''
# Function to get the Factorials of a number.
def get_factorial(num):
if (num == 0) :
return 1
else:
return num * get_factorial(num-1)
def combi(n,r):
fn = get_factorial(n)
fr = get_factorial(r)
fnr = get_factorial(n-r)
return fn / (fr*fnr)
# To store the values more than 1 million.
values_over_1m =[]
nn = 1
rr = 1
start_value= combi(nn,rr)
stop_me = False
while stop_me == False :
nn +=1
rr =2
while rr < = nn :
start_value = combi(nn,rr)
if start_value >1000000 :
values_over_1m.append([nn,rr])
rr +=1
if nn > 99 :
stop_me = True
print(‘Ther is ‘,len(values_over_1m),’ Values meeting the equation.’)

|
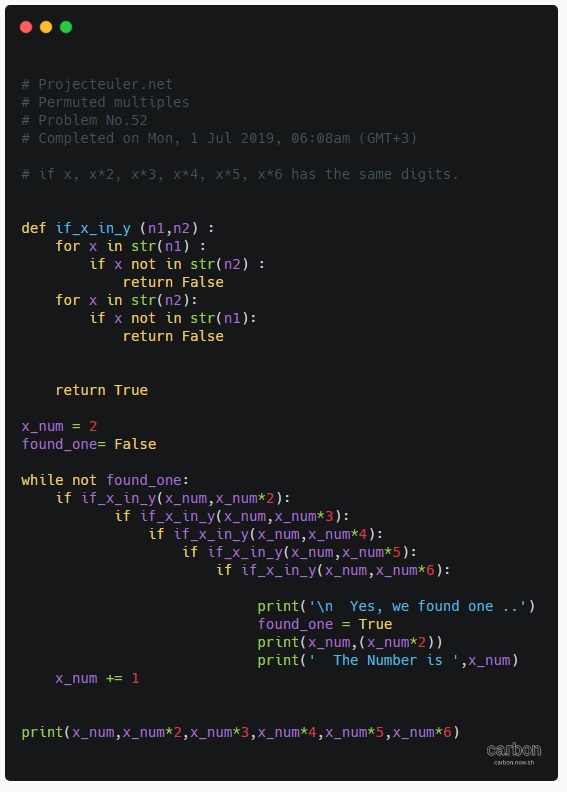
Python: Permuted Multiples
Python: Permuted Multiples
Problem No.52 @ Projecteuler
This task Completed on Mon, 1 Jul 2019, 06:08, the goal is to find a number X that if we get the X, X*2, X*3, X*4, X*5, X*6 all the numbers are same digits but in a different order.
I use a function called if_x_in_y (n1,n2) will return True if the two numbers has same digits, False if not. Then a while found_one is not True a loop will examine all numbers starting from 2 until we found_one.

|
The Code:
# Projecteuler.net
# Permuted multiples
# Problem No.52
# Completed on Mon, 1 Jul 2019, 06:08am (GMT+3)
# if x, x*2, x*3, x*4, x*5, x*6 has the same digits.
def if_x_in_y (n1,n2) :
for x in str(n1) :
if x not in str(n2) :
return False
for x in str(n2):
if x not in str(n1):
return False
return True
x_num = 2
found_one= False
while not found_one:
if if_x_in_y(x_num,x_num*2):
if if_x_in_y(x_num,x_num*3):
if if_x_in_y(x_num,x_num*4):
if if_x_in_y(x_num,x_num*5):
if if_x_in_y(x_num,x_num*6):
print(‘\n Yes, we found one ..’)
found_one = True
print(‘ The Number is ‘,x_num)
x_num += 1
print(x_num,x_num*2,x_num*3,x_num*4,x_num*5,x_num*6)
|
Python: Number Letter Counts
Python: Number Letter Counts
Problem 17, Projecteuler
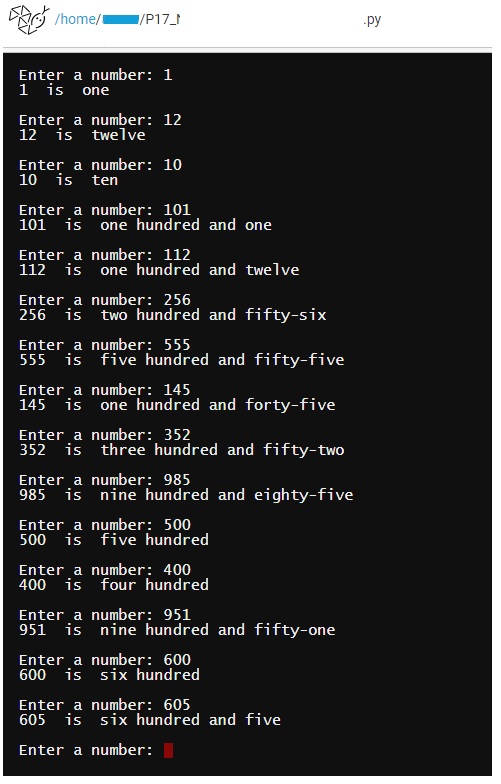
For problem 17, projectEuler ask for the total numbers of alphabetics in all words of numbers from 1 to 1000.
Here I am coping from there page.
Once I read the task, I decide to create my own version of the requirement. I start to assume that I may have a dictionary with some numbers and words, then base on what ever the user will input (number between 1 and 999) then I shall convert it to words.
Example:
1 –> one
8 –> eight
234 –> tow hundred thirty-four .. and so on.
I start searching the net to get the words I need, and store them in 3 dictionaries.
num_1_9 = {“1″:”one”,”2″:”two” .. ext.
num_10s = {“10″:”ten”,”20″:”twenty” .. ext.
num_11s = {“11″:”eleven”,”12″:”twelve”.. ext
Then, I start writing the functions for each group of numbers/dictionaries, so if the user enter a number we will read number of digits if it is 1 then we call def num_1_d(), if it is 2 digits we call def num_2_ds() and if it is 3 digits we call num_3_ds(). At the end, we got the right answer for Projecteuler, and here is the code in my way, I am asking the user to enter a number then i convert it to a corresponding words.

|
The Code:
# Date:27/6/2019
# ProjectEuler
# Problem No.17
# Completed on Sun, 30 Jun 2019, 10:30
num_1_9 = {“1″:”one”,”2″:”two”,”3″:”three”,”4″:”four”,”5″:”five”,”6″:”six”,”7″:”seven”,”8″:”eight”,”9″:”nine”}
num_11s={“11″:”eleven”,”12″:”twelve”,”13″:”thirteen”,”14″:”fourteen”,”15″:”fifteen”,”16″:”sixteen”,”17″:”seventeen”,”18″:”eighteen”,”19″:”nineteen”}
num_10s ={“10″:”ten”,”20″:”twenty”,”30″:”thirty”,”40″:”forty”,”50″:”fifty”,”60″:”sixty”,”70″:”seventy”,”80″:”eighty”,”90″:”ninety”}
num_100=’hundred’
def num_1_d(num):
if len(str(num)) == 1:
return num_1_9[str(num)]
def num_2_ds(num):
d0,d1 = num[0], num[1]
if int(num[1])== 0 :
return num_10s[str(num)]
elif int(num[0]) == 1 :
return num_11s[str(num)]
elif (int(num[0])) >1 :
d0=str(d0)+str(0)
return ‘{}-{}’.format(num_10s[str(d0)],num_1_9[str(d1)])
def num_3_ds (num):
d0,d1,d2=num[0],num[1],num[2]
if (int(num[1])==0) and (int(num[2])==0) :
return ‘{} {}’.format(num_1_9[str(d0)],num_100)
elif (int(num[1])>0):
d1 = str(d1)+str(d2)
return ‘{} {} and {}’.format(num_1_9[str(d0)],num_100,num_2_ds(d1))
elif (int(num[1])==0) and (int(num[2])>0):
d1 = str(d1)+str(d2)
return ‘{} {} and {}’.format(num_1_9[str(d0)],num_100,num_1_9[str(d2)])
num =0
while num !=’f’ :
num =input(‘\nEnter a number: (1-999)’)
if len(str(num)) == 1:
print(num ,’ is ‘,(num_1_d(num)))
elif len(str(num)) == 2:
print (num ,’ is ‘,(num_2_ds(num)))
elif len(str(num)) == 3:
print (num ,’ is ‘,(num_3_ds(num)))
This is Output screen for my-way version
|
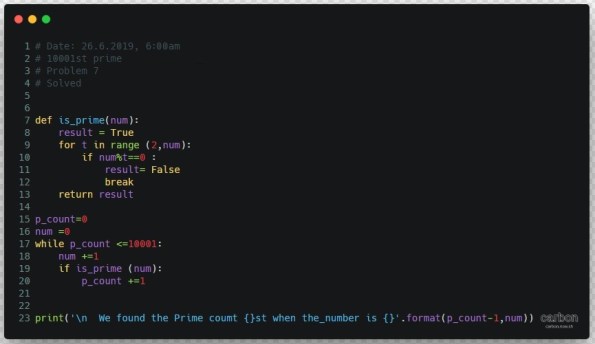
Python: 10001st Prime
Python: 10001st Prime
Problem No.7 @ ProjectEuler
This is one of shot projects you may find on ProjectEuler, the task is find the prime No 10001, I just run my is_prime function, if the number is prime will add 1 to the counter, until we reach 10001, that will be the answer.

|
The Code:
# 10001st prime
# Problem 7
# Solved: Wed, 26 Jun 2019, 05:57am (GMT+3)
def is_prime(num):
result = True
for t in range (2,num):
if num%t==0 :
result= False
break
return result
p_count=0
num =0
while p_count <=10001:
num +=1
if is_prime (num):
p_count +=1
print(p_count,num)
print(num,p_count-1)
Python Project: Split and join
Python: Split and join
Split up the message on newline
The target of this task is to Split a given text message on the newline (\n) then use the join builtin to stitch it together using a ‘|’ (pipe).
I fond this on the pybites web-site as a code-challenges bites #104. In our case we will print the new Message within the function but we can return it back as a variable for more usage in our code..
Enhancements: If we want to do some enhancements to this code:
1. We can read the message from a file.
2. Letting the user to select the joining character.
3. Also we may export the final message to another txt file.
We assume our message is “Hello world!\nWe hope that you are learning a lot of Python.\nHave fun with our Bites of Py.\nKeep calm and code in Python!\nBecome a PyBites ninja!”
The Code:
def split_in_columns(message=message):
sp_message = message.split(“\n”)
message=”|”.join(sp_message)
print(message)
split_in_columns(message=message)
Python: Digit Factorial Chains
Python: Digit factorial Chains
Problem No.74 @ ProjectEuler
In this task, we need to produce a chain of the summation of a factorial number and keep chasing each number in the chain until it starts repeat, we stop there and count the length of the chain, if its 60 then we increase a counter. ProjectEuler task 74 ask to do this and get all the numbers (How many are they?) below one Million (1000000) that has 60 numbers in it’s chain.
So we start to write two functions, one to get the factorial of a number, and the other to get the summation of the numbers in a list. Then with two (while) loop, an outer one to count the 60’s chain numbers, and an inner one to produce the chains.
At the end we manage to solve the problem 74 using Pythonanywhere.

|
The Code:
#Digit factorial chains
#Problem 74
numbers=[]
# Function to get the Factorials of a number.
def get_factorial(num):
if (num == 0) :
return 1
else:
return num * get_factorial(num-1)
def get_summation(the_list):
tot=0
for each in the_list:
tot +=each
return tot
start_num = 2
the_num = start_num
keep_chain=[start_num]
chain_count = 0
print(‘We start with number ‘,start_num)
the_facto_d_sum = 0
while start_num < 1000000 :
the_num = start_num
keep_chain=[start_num]
while the_facto_d_sum != start_num:
for each in str(the_num):
numbers.append(get_factorial(int(each)))
the_facto_d_sum = get_summation(numbers)
the_num = the_facto_d_sum
if the_num in keep_chain :
the_facto_d_sum = start_num
else:
keep_chain.append(the_num)
numbers=[]
if len(keep_chain) == 60:
chain_count +=1
keep_chain =[]
start_num +=1
print(‘we have {} numbers with 60 ‘.format(chain_count))
Python: 1000-Digit Fibonacci
Python: 1000-Digit Fibonacci
Problem No.25, ProjectEuler
Another easy fast 5-minites task on projecteuler that Playing around Fibonacci Numbers, the task is to find the first Fibonacci index to contain 1000 digits.
So we will write a function to get the fibonacci numbers and each time we will check if it’s digits reach 1000, if not we will go for generating the next number.

|
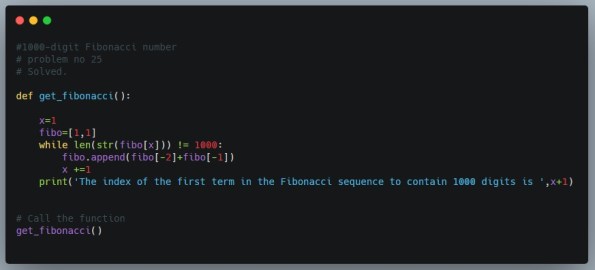
The Code:
#1000-digit Fibonacci number
# problem no 25
# Solved.
def get_fibonacci():
x=1
fibo=[1,1]
while len(str(fibo[x])) != 1000:
fibo.append(fibo[-2]+fibo[-1])
x +=1
print(‘The index of the first term in the Fibonacci sequence to contain 1000 digits is ‘,x+1)
# Call the function
get_fibonacci()
|
Python: Distinct Powers
Python: Distinct Powers
ProjectEuler Problem No.29
In this project we have a sequance of numbers based on a powered number, it takes ten minites or less to write the code, test it and applay the needed figures to solve the problem. Thie code can be shorten, but I am using the classic way to write functions with comments on code.
Here is the Problem as on the ProjectEuler Portal:
Consider all integer combinations of ab for 2 ≤ a ≤ 5 and 2 ≤ b ≤ 5:22=4, 23=8, 24=16, 25=32
32=9, 33=27, 34=81, 35=243
42=16, 43=64, 44=256, 45=1024
52=25, 53=125, 54=625, 55=3125
If they are then placed in numerical order, with any repeats removed, we get the following sequence of 15 distinct terms:4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125
How many distinct terms are in the sequence generated by ab for 2 ≤ a ≤ 100 and 2 ≤ b ≤ 100?

|
The Code:
#Distinct powers
#Problem 29
sequence_list=[]
def get_sequence (a):
for b in range (2,101):
if a**b not in sequence_list:
#If the elements NOT exist in the list then add it.
sequence_list.append(a**b)
for a in range (2,101):
get_sequence (a) # Calling the function
# Get the total elements in the sequence_list
print (len(sequence_list))

|
 Follow me on Twitter..
Follow me on Twitter..